14-3. 로지스틱 회귀분석
(Logistic Regression)
1) 로지스틱 회귀모형
Y : Remiss (0, 1) <- 타겟 변수가 0, 1로 됨
6 explanatory variable : risk factor related cancer remission (Cell, Smear, infill, Li, blast, temp)

- 로지스틱 회귀분석 (logistic regression)은 종속변수가 범주형인 경우 사용되는데 2개의 범주 (양성/음성, 불량/양품 등) 혹은 3개 이상의 범주를 다루기도 한다. 3개 이상의 범주의 경우 서열형 데이터(ordinal data)인 경우와 명목형 데이터(nominal data)에 따라 다른 모형이 사용된다.

- Y가 (0/1, cancer/np cancer, present/absent) 등의 값을 취하는 경우, 다음과 같은 로지스틱함수가 독립변수들과 Y간의 관계를 설명하기 위해 사용된다.
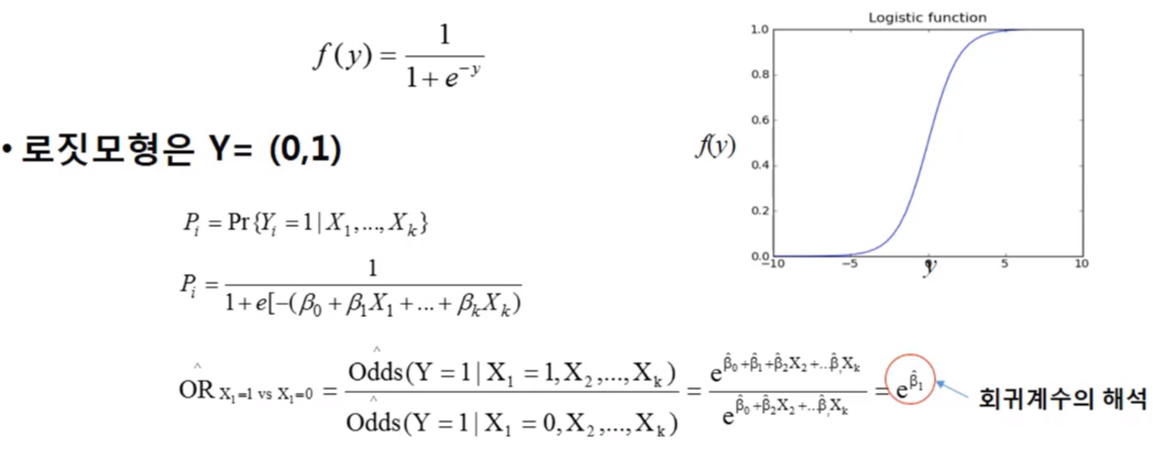
2) 로지스틱 회귀모형 - 예제
로지스틱 회귀모형 : y는 binomial variable, logit function 선택
t1<-glm(remiss~cell+smear+infil+li+blast+temp, data=re,family=binomial(logit))
summary(t1)
cor(re)

1에 가까움 -> 설명되어질 필요X
- 로지스틱 회귀모형의 평가척도 : ~2Log (Deviance), AIC, likelihood ratio test(G^2)
t2<-glm(remiss~cell+smear+li+temp, data=re,family=binomial(logit))
summary(t2)

AIC가 낮은 모델이 더 좋은 모델로 평가
smear변수의 Pr값이 높음 -> smear변수 제외하고 다시
t3<-glm(remiss~cell+li+temp, data=re,family=binomial(logit))
summary(t3)
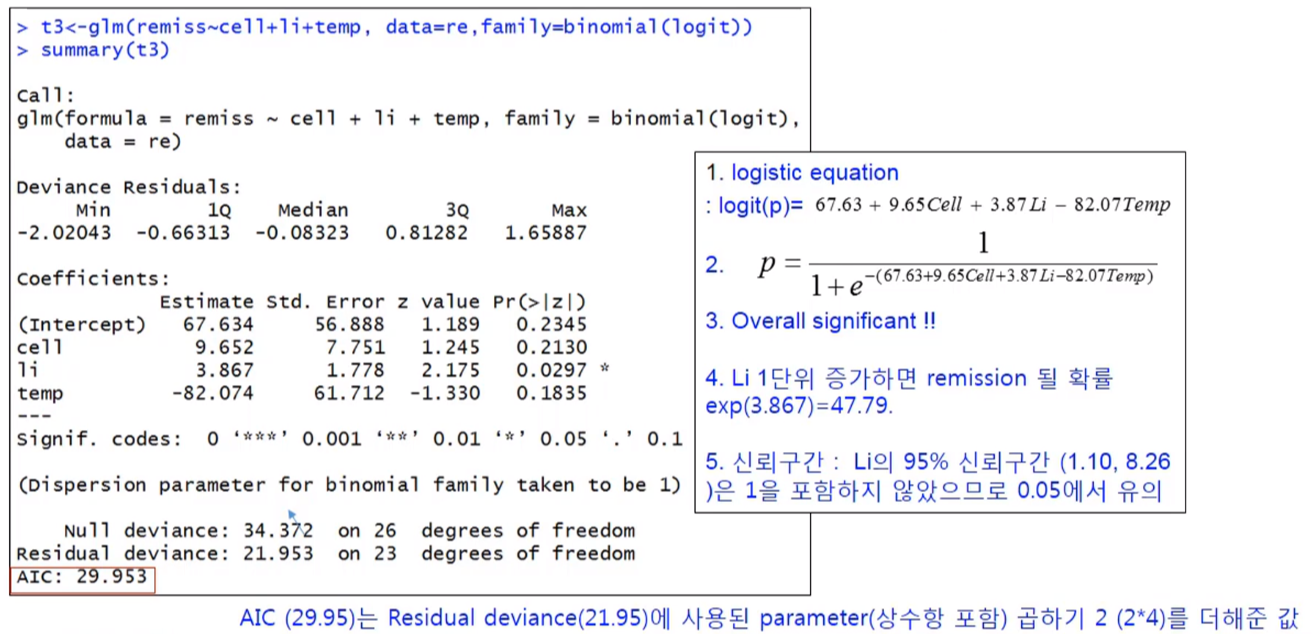
[예제] 계속
위의 결과에 대한 추정회귀식은 다음과 같다.
logit(P)=67.64 + 9,65 Cell + 3.87 li - 82.07 temp
Cell=1 이고 li=1.2, temp=.99 이면,
logit(P)=67.64+9.65*1+3.87*1.2-82.07*.99 = 0.68

- 예측확률값 출력 : 원래 데이터 + 예측확률값
dat1_pred<-cbind(re,t3$fitted.values)
write.table(dat1_pred,file="dat1_pred.csv", row.names=FALSE, sep=",", na=" ")

'공부 > R & Python' 카테고리의 다른 글
| 15-2. 주성분 회귀분석(Principle Component Regression) (0) | 2020.03.06 |
|---|---|
| 15-1. 주성분 분석과 부분 최소자승법-주성분분석(Principle Component Analysis) (0) | 2020.03.06 |
| 14-2. 연관규칙 분석 2 (0) | 2020.03.05 |
| 14-1. 연관규칙과 로지스틱회귀분석-연관규칙 분석 1(Association Rule Analysis) (0) | 2020.03.05 |
| 13-3. 군집분석 - 비계층적 군집분석 - (0) | 2020.03.05 |



