13. 군집분석
13-1. 군집분석과 유사성척도
1) 군집분석
- 군집분석은 비지도학습(Unsupervised Learning) : 속성변수들의 특징으로 그룹화
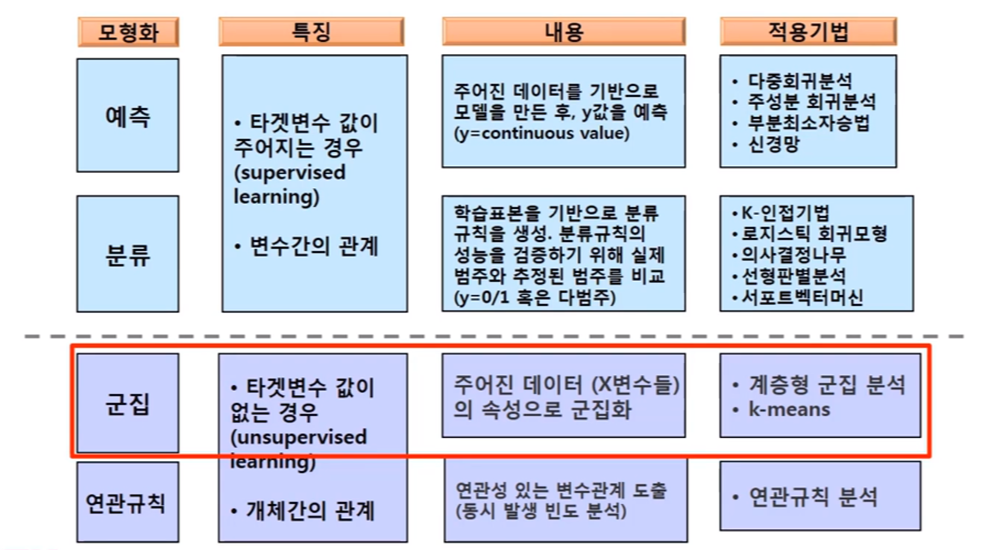
- 군집분석(cluster analysis)이란, 유사한 속성을 가진 객체들을 군집(cluster)으로 나누는(묶어주는) 데이터마이닝 기법
- 예제 : 고객들의 구매패턴을 반영하는 속성들에 관한 데이터가 수집된다고 할 때
=> 군집분석을 통해 유사한 구매패턴을 보이는 고객들을 군집화하고 판매전략을 도출

2) 군집분석 종류
- 군집분석의 방법은 (1) 계층적 방법과 (2) 비계층적 방법으로 구분

군집분석
- 유사성척도의 계산-
1) 유사성 척도
- 객체 간의 유사성 정도를 정량적으로 나타내기 위해서 척도가 필요
- 거리(distance) 척도
거리가 가까울수록 유사성이 크다. 거리가 멀수록 유사성이 적어짐
- 상관계수척도
객체간 상관계수가 클수록 두 객체의 유사성이 커짐
2) 거리척도

3) 유클리디안 거리

- 거리(distance) 계산 함수 : dist(데이터, method= , )
m1 <- matrix(
c(150, 50, 130, 55, 80, 80, 100, 85, 95, 91),
nrow = 5,
ncol = 2,
byrow = TRUE)
데이터 생성 (m1, 5x2 행렬)
m1<-as.data.frame(m1)
m1을 data frame으로 저장
D1 <- dist(m1) default가 유클리디안 거리
D1
- 거리계산 옵션
help("dist")
4) 그 외 거리 척도
- 민코프스키 거리(Minkowski distance)
- 유클리디안 거리의 일반화된 방법 (m=2 일 때는 유클리디안 거리와 동일)

- 마할라노비스 거리(Mahalanobis distance)
- 변수 간의 상관 관계가 존재할 때 사용

- 민코프스키 거리(Minkowski distance)
: dist(data(or matrix), method="minkowski", p=3)
D2<- dist(m1, method="minkowski", p=3)
D2
민코프스키 계산식에서 p=2이면 유클리디안거리와 동일
5) 상관계수를 척도로 사용
- 또 다른 유사성 척도로 객체 간의 상관계수를 사용
- 상관계수가 클수록 두 객체의 유사성이 크다고 추정
- 객체 i와 객체 j 간의 표본상관계수는 다음과 같이 정의

- 상관계수측정(cor)
m2 <- matrix(
c(20, 6, 14, 30, 7, 15, 46, 4, 2),
nrow = 3,
ncol = 3,
byrow = TRUE)
데이터 생성 ( 3x3 matrix )
cor(m2[1,],m2[2,])
cor(m2[1,],m2[3,])
상관계수 측정
객체1(obs1)과 객체2의 유사성이
객체1(obs1)과 객체3간의 유사성보다 크다 (0.9674 > 0.7984)
'공부 > R & Python' 카테고리의 다른 글
| 13-3. 군집분석 - 비계층적 군집분석 - (0) | 2020.03.05 |
|---|---|
| 13-2. 군집분석 - 계층적 군집분석 - (0) | 2020.03.05 |
| 12-3. 랜덤포레스트 (Random Forest) (0) | 2020.03.04 |
| 11-2. 의사결정나무 (Decision Tree) 2 (0) | 2020.03.04 |
| 12-1. 의사결정나무와 랜덤 포레스트-의사결정나무 (Decision Tree) 1 (0) | 2020.03.04 |



